VR头显视场的定量比较:视场实际测量的是什么?
VR头显的定量比较
(映维网 2020年02月03日)美国加州大学戴维斯分校的研究类计算机科学家奥利弗·克雷洛斯(Oliver Kreylos)的博客从开发者角度(非用户角度)讨论了有关沉浸式计算机图形学的方方面面,并为行业提供了一定的参考借鉴。日前,克雷洛斯撰文介绍了VR头显视场的定量比较。下面是映维网的具体整理:

尽管我已经用校准过的广角相机拍摄了多款常见VR头显的镜后图片,但我一直努力构思如何能够定量地比较最终的视场,如何将它们放到具体的情景进行理解,以及如何适当地形象化它们。当尝试回答“哪款VR头显的视场更大?”,“头显A的视场比头显B的视场大多少?”或“头显C的视场与人眼相比又如何?”的时候,你面对的一个基本问题是:如何以一种公平的方式并在各种可能尺寸范围内比较视场。如果有人提出单一的角度,我们应该如何衡量?比如说“对角线”视场?如果视场不是矩形呢?如果有人提出两种角度,例如水平⨉垂直呢?同样,如果视场不是矩形呢?
然后,如果是以单一的角度或两个角度来衡量视场,我们又应该如何公平地比较不同的视场呢?如果一款头显的视场是100度,而另一款头显是110度,这是否意味着后者显示的虚拟3D环境要多出10%呢?如果一款头显的视场是100度⨉100度,而另一款的视场为110度⨉110度,这是否意味着后者显示的虚拟3D环境要多出21%呢?
为了寻找合理的答案,我们先从基本定义入手:视场实际测量的是什么?基本上,视场是衡量观察者在任何给定瞬间能够看到多少虚拟3D环境。较大的视场值应表示可以看到更多。理想情况下,两倍的视场值应表示可以看到两倍的视像。
“能够看到”是什么意思?如果来自某物的光纤到达我们的眼睛,通过角膜,瞳孔和晶状体,最后到达视网膜,这时我们就可以看到它。原则上,光线会从所有可能的方向传播到我们的眼睛,但由于各种障碍(例如,我们看不到背面),只有来自一部分方向的光线会到达视网膜。所以,合理的视场测量(一只眼睛)应该是来自不同3D方向并到达眼睛视网膜的光线的总和。问题是,光线可以来自于无数个不同的方向,所以简单的计数不起作用。
1. 立体角
另一种思考方式是,在观察者眼睛周围放置一个任意半径的假想球体,球体中心与眼睛瞳孔重合。这样,3D方向和所述假想球体的点之间将存在一一对应的关系:每条光线恰好通过一个点进入球体。结果是,无需计算3D方向,你可以将视场化作球体所有点的集合的总面积,所述点对应于眼睛可以看到的3D方向。
碰巧的是,如果假想球体的任意半径设为1,这正是立体角的定义(立体角是一个物体对特定点的三维空间的角度,是平面角在三维空间中的类比。它是指站在某一点的观察者测量到的物体大小的尺度。若以观察点为球心构造一个单位球面,任意物体投影到所述单位球面的投影面积即为所述物体相对于所述观察点的立体角。)。如果什么都看不到,即球体所有“可见”点的集合为空,则所述集合的面积为零。如果可以看到所有一切,则可见点的集合就是球体的整个表面,其面积为4π。如果仅能看到所有内容的一半(如由于观察者站在无限平面之上),则观察者的视场为2π,依此类推。顺便一提,若球体半径为1,其表面积属于无单位(没有度量单位),但为了将立体角值与其他无单位的数值区分开来,我们用球面度(steradian;sr)作为单位,与以弧度(r)或度数(°)给出的规则(2D)角度(基本为无单位)相同。
总而言之,立体角是测量视场的可靠方法:它可以在单个数字中测量任意形状和大小的视场,并且所述数字与“可见”量之间存在直接的线性关系。
2. 立体角和VR头显视场
我们迄今已经讨论过视界,即“裸眼”可以看到多少3D环境。如下所示,这个数字本身十分重要,但真正的问题是如何衡量VR头显的视场。总体的思路相同:计算用户可以看到多少虚拟3D环境。但与真实3D环境不同,虚拟环境发出的光线不会从所有可能的方向到达观察者眼睛。相反,光线仅来自于显示屏。若从眼睛向后回溯,光线会穿过头显的一个透镜,并最终到达所述透镜后面的显示屏。视场依然以相同的方式计算,但现在是向后:视场是用户眼睛周围的单位球面的所有点的面积,点对应于来自屏幕的方向(假设屏幕的该点是用于由VR管道显示图像数据,但这是另一个问题)。
幸运的是,我们可以以相当简单的方式来测量这个面积。所有相机都会将3D环境投影到成像表面(光板或光敏传感器),特别是将通过相机焦点入射的3D方向分配给成像表面的每个点。在经过校准的相机中,从图像点到3D方向的映射是精确已知(具体的计算方法将是另一篇文章的主题)。
具体的方法是,将这种经过校准的相机(理想情况是带有广角的相机)放置在头显透镜前方,模拟用户穿戴头显并通过透镜感知虚拟环境的情形,然后拍照通过透镜看到的画面。接下来,查看每个图片像素,确定一个像素是否显示了屏幕的某个部分,并就所有像素的立体角求和(最后一点有点复杂,并可作为读者的一项练习)。但最重要的是所拍摄的图片。
3. 可视化VR头显的视场
为给定的头显计算单个立体角很适合进行定量比较,但一张图片胜过千言万语。所以,如何以公平的方式可视化视场呢?毕竟,视场是球体表面的一部分面积,而且任何熟悉世界地图的人都清楚,如果不引入变形,你无法在平面图像显示球体表面。幸运的是,有一类地图投影可以保留面积,换句话说,投影地图中的某个区域的面积与球体相同区域的面积成比例,或者理想情况下相同。鉴于立体角或球面面积是视场的合理度量,使用这种保留面积的投影应该可以产生清晰的可视化效果:如果一款头显的视场是另一头显的两倍,图片所示就会恰好是两倍。
4. 汇总整合
对于本文,我测量了我碰巧拥有的三款VR头显的视场:HTC Vive Pro,Oculus Rift CV1和PSVR。我同时以相同的方式并根据常用的表格(图1)测量了人类裸眼视场的“平均”值。
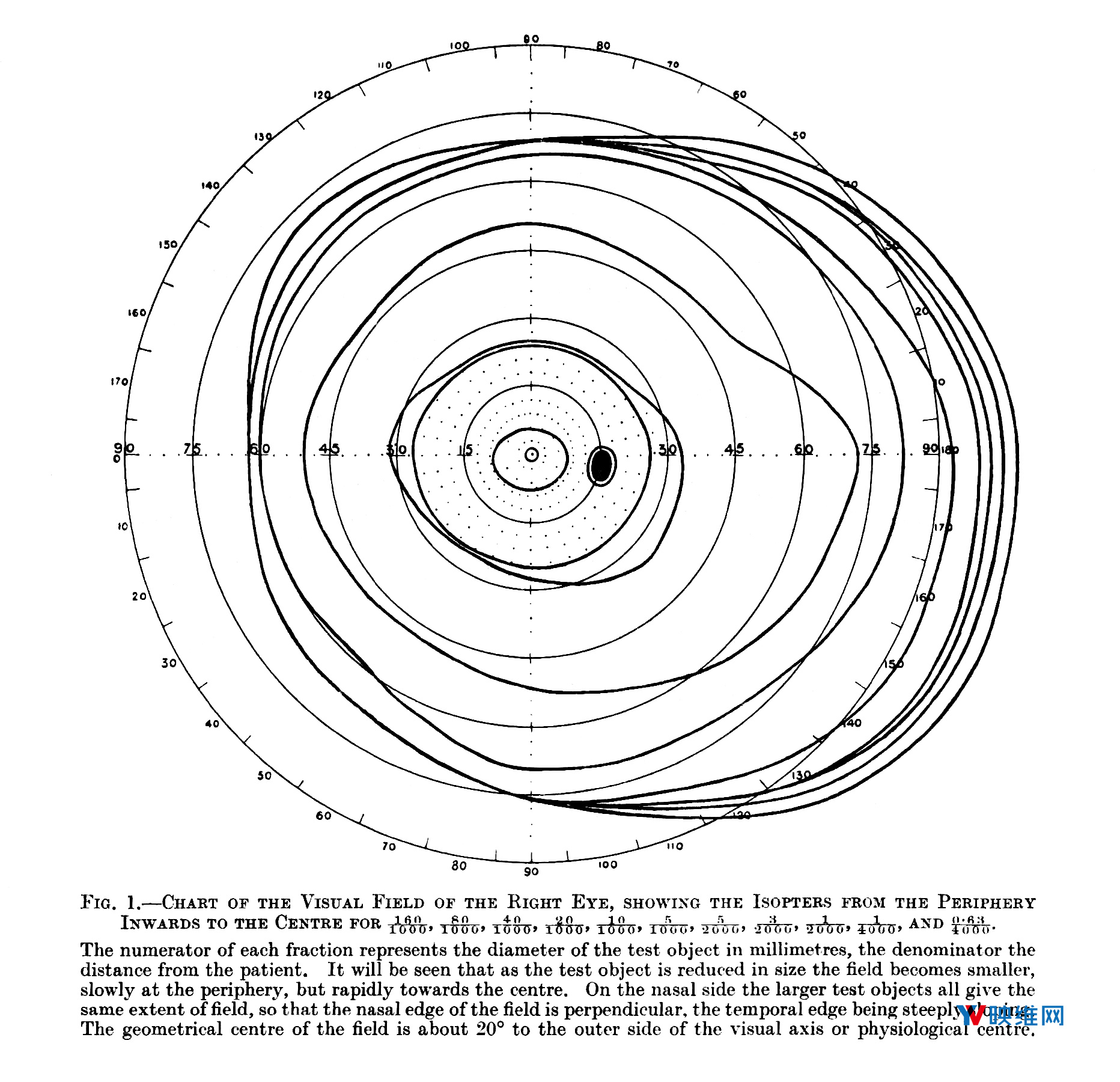
图1:右眼的视野,出自亨利·莫斯·特拉奎尔(H. M Traquair)的《临床视野测量法导论(An Introduction to Clinical Perimetry)》第一章。上图是等距方位角投影,不同于本文使用的面积保留投影。
我回溯了图中视野的外部界限,将轮廓重新投影到面积保留投影中(参见图2),并计算了其立体角,即两只眼睛的总立体角(假设两个视场为对称),以及双眼视场相交的立体角,即双眼重叠。具体的数值如下:一只眼睛是5.2482 sr(或1.6705πsr);双眼是6.5852 sr(或2.0961πsr);重叠是3.9112(或1.2450πsr)。我采用的直接球面度数值和π次方球面度数值,以防后者更易于可视化:2πsr是半球,而4πsr是完整球体。有趣的是,两只眼睛的合并视场略大于半球。尽管视场因人而异,但这种平均测量数值可用于具体描述VR头显的视场值。
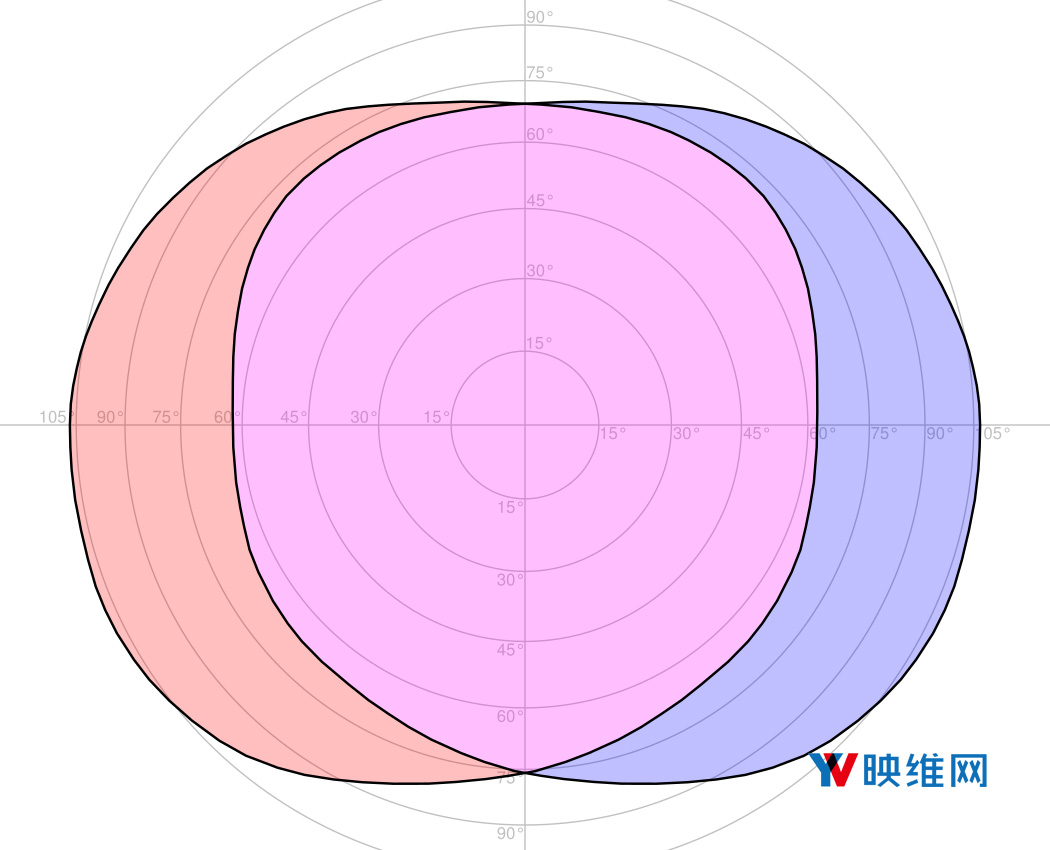
图2:面积保留投影中的人类平均裸眼视场,包括眼球运动;数字表示距离正向的方位角;红色是左眼视场,蓝色是右眼视场;紫色是双目视场(立体重叠)。
接下来,我以相同的方式处理了三款头显的镜后图片,回溯屏幕可见部分的轮廓,使用相同的面积保留投影重新投影轮廓,计算单眼、双眼和重叠立体角(参见表1),并将视场叠加到普通人眼的视场(参见图3-5)。如图所示,对于每款头显,我只使用最大化视场的适眼距值。鉴于视场非常依赖于眼睛的适眼距,所以理想情况下应该拍摄一系列的照片并列出适眼距。
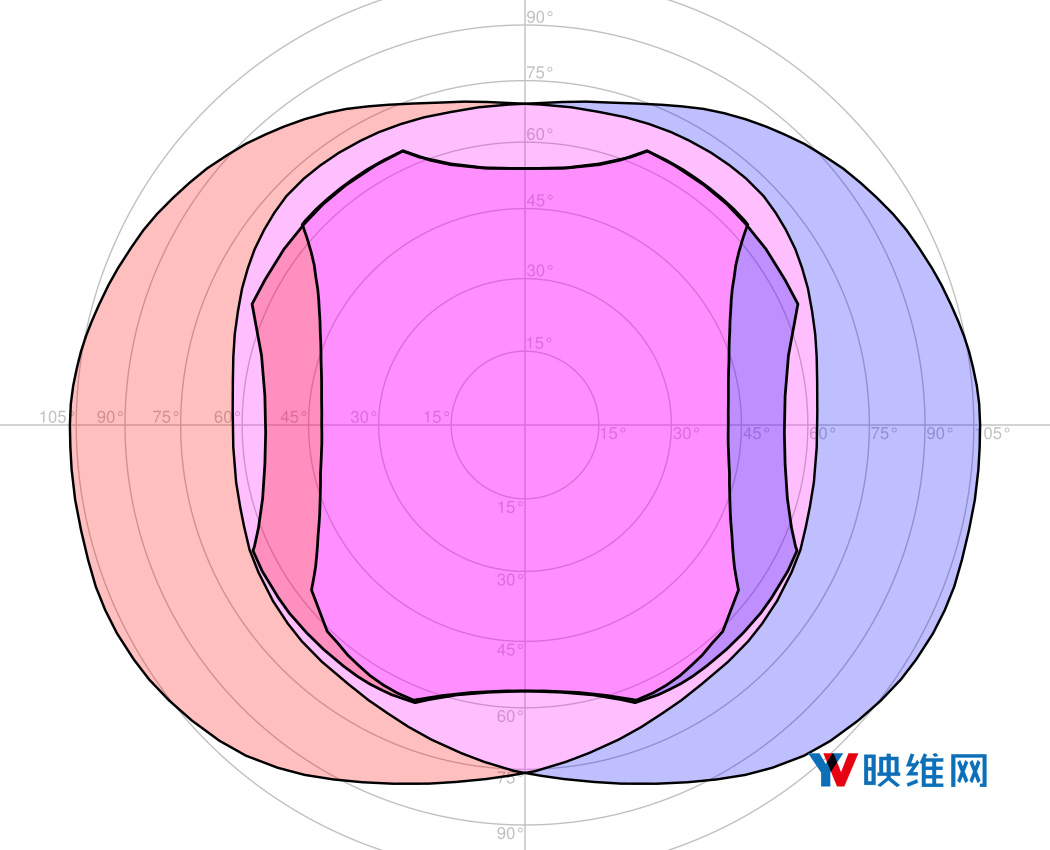
图3:使用面积保留投影将HTC Vive Pro的最大视场(适眼距8mm)叠加在平均人类视场;数字表示距离正向的方位角;红色是左眼视场,蓝色是右眼视场;紫色是双目视场(立体重叠)。
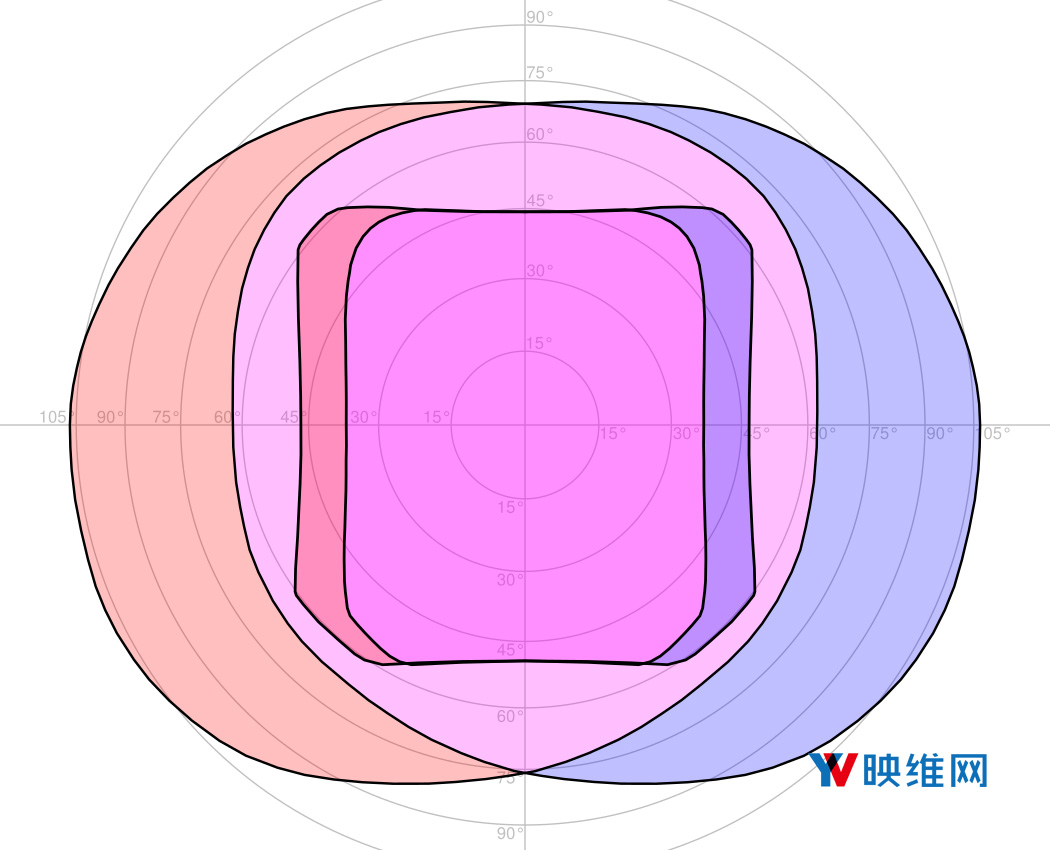
图4:使用面积保留投影将Oculus Rift CV1的最大视场(适眼距15mm)叠加在平均人类视场;数字表示距离正向的方位角;红色是左眼视场,蓝色是右眼视场;紫色是双目视场(立体重叠)。
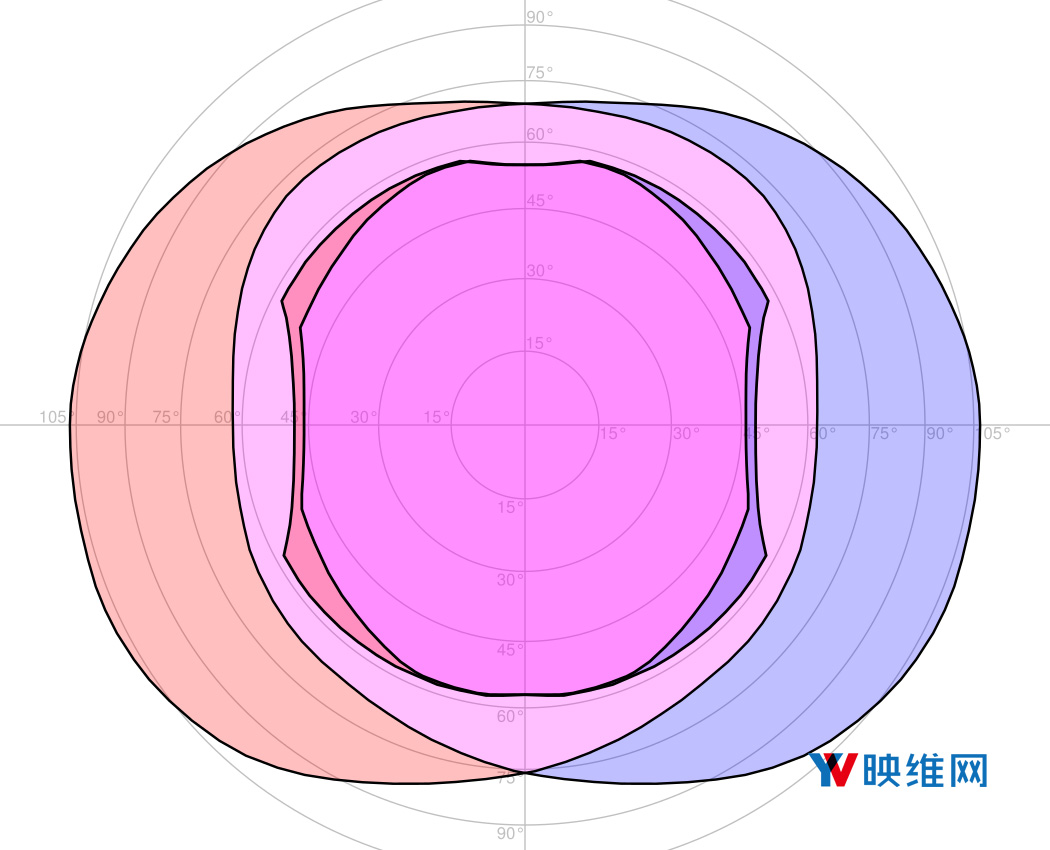
图5:使用面积保留投影将PSVR的最大视场(适眼距10mm)叠加在平均人类视场;数字表示距离正向的方位角;红色是左眼视场,蓝色是右眼视场;紫色是双目视场(立体重叠)。
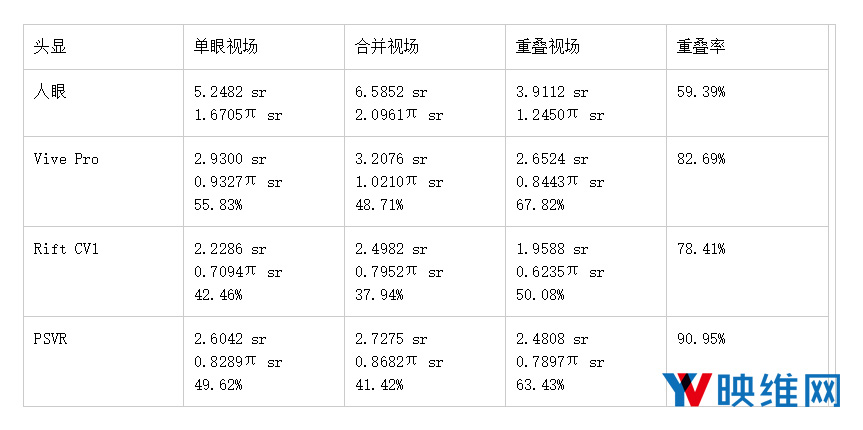
表1:平均人类视场(包括眼睛运动)和三款VR头显的视场。每个视场测量值均以球面度和π次方球面度给出。头显视场测量值同时以平均人类视场的相应测量值的百分比给出。