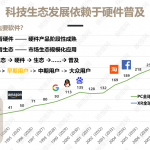
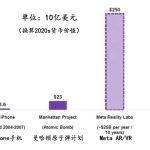
Meta研究结合参数化声场改进AR/VR音频双耳信号匹配性能
研究和分析了具有参数化声场的BSM在时频域的性能
（映维网Nweon 2022年11月10日）对于AR/VR，听觉是实现沉浸感的一块重要拼图。通过麦克风阵列捕获的声学场景双耳再现越来越流行，并在AR/VR中存在一系列的应用。
双耳再现的一种热门方法涉及将High Order Ambisonics（HOA）信号与头相关传递函数（HRTF）卷积。这种方法对于足够高的球面谐波（Spherical Harmonics/SH）order相当准确，并且头部追踪的结合增强了沉浸体验。但所述方法的主要缺点在于，当通过球形麦克风阵列记录音频信号时需要大量麦克风，并且需要球形阵列几何形状，这限制了它的实际使用。
为了使用更灵活的阵列几何形状来再现双耳信号，社区曾提出了基于波束成形的双耳再现（Beamforming-based Binaural ReproductionBFBR）。所述方法使用一组波束成形器对麦克风信号进行滤波，然后再使用HRTF对输出信号进行滤波，并且求和以再现双耳信号。然而，对于更一般的阵列几何结构，它只能带来有限的指导原则，无法保证准确的双耳信号再现。
为了克服基于波束成形方法的局限性，并准确再现由任意几何阵列记录的双耳信号，社区又开发了双耳信号匹配（Binaural Signal-Matching/BSM）方法。其中，BSM使用分别为每个耳朵计算的最佳滤波器直接从阵列测量中估计双耳信号。不过，BSM的精度对传声器位置而不是其数量敏感。特别是，阵列中的麦克风离耳朵越近，耳朵中的双耳再现效果越好。所以，BSM方法的主要缺点是它在高频下表现不佳，尤其是在其中一只耳朵距离阵列的所有麦克风相对较远的情况下。
......（全文 2322 字，剩余 1785 字）
请微信扫码通过小程序阅读完整文章或者登入网站阅读完整文章
映维网会员可直接登入网站阅读
PICO员工可联系映维网免费获取权限
